Soal dan Jawaban Latihan 4.2 Kekongkruenan Dua Segitiga, Matematika Kelas 9

Soal dan Jawaban Latihan 4.2 Kekongkruenan Dua Segitiga, Matematika Kelas 9.~ m4thguru.info, assalamualaikum Wr Wb, Salam Sejahtera untuk kita semua, kali ini kkaktri akan postingan lagi tentang soal dan kunci Jawaban Soal Ayo kita Berlatih Matematika kelas 9 yang diambil dari buku paket matematika kurikulum 2013 revisi 2018. untuk soal kali ini tentang memahami Kesebangunan, soal ada di halaman 226- 228 buku matematika kelas 9 Bab 4 tentang Kekongkruen. untuk jawaban kkaktri sendiri yang menjawab dan sengaja di share sebagai bahan evaluasi adikadik setelah mengerjakan soal tersebut.

Soal dan Jawaban Latihan 4.2 Kekongkruenan Dua Segitiga, Matematika Kelas 9

Latihan 4.2 Hal 226 - 228

1. Perhatikan gambar di bawah ini. Tunjukkan bahwa ∆PQS dan ∆RQS kongruen.

Jawaban

1. PQ = RQ (diketahui pada gambar)
QS (pada ∆PQS) = QS (pada ∆RQS) (berhimpit)
PS = RS (diketahui pada gambar)
Jadi, ∆PQS dan ∆RQS kongruen berdasarkan kriteria sisi – sisi – sisi.

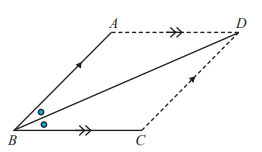
2. Perhatikan gambar di bawah ini. Panjang AB = DE dan AB//DE. Buktikan bahwa ∆ABC dan ∆EDC kongruen.

Jawaban :

Buktikan dengan kriteria sudut – sisi – sudut atau dengan kriteria sisi – sudut – sudut.
Pembuktian ∆ ABC dan ∆ EDC kongruen

AB = DE
∠DCE = ∠ACB (bertolak belakang)
∠ ABC =∠CDE (berseberangan)

kreteria : sisi, sudut, sudut

3. Titik C adalah titik pusat lingkaran. Tunjukkan bahwa dua segitiga pada gambar di samping adalah kongruen.

Jawaban :
CA = CB = jari-jari lingkaran
m∠ACB = m∠ECD (bertolak belakang)
CD = CE = jari-jari lingkaran
Jadi, ∆ACB dan ∆ECD kongruen berdasarkan kriteria sisi – sudut – sisi.

4. Bangun WXYZ adalah segi empat dengan sisi-sisi W X Z Y yang berhadapan panjangnya sama. XZ adalah salah satu diagonalnya.
a. Buktikan bahwa ∆WXZ ≅ ∆ZYX.
b. Tunjukkan bahwa WXYZ adalah jajargenjang.

Jawaban

 a. Buktikan dengan kriteria sisi – sisi – sisi.
b. Gunakan kekongruenan ∆WXZ dan ∆ZYX
karena ∆WXZ ≅ ∆ZYX (berdasarkan kriteria sisi – sisi – sisi)

berarti karena m∠WXZ = m∠YZX dan m∠WZX = m∠YXZ, maka m∠ZWX = m∠XYZ .... (i)

                       m∠WZX = m∠YXZ   ...(ii)

                       m∠XWZ = m∠ZYX  ...(iii)

Berdasarkan (i), (ii), dan (iii) berarti WXYZ adalah jajargenjang

5. Perhatikan gambar di bawah ini. Titik O adalah pusat lingkaran dalam dan lingkaran luar. AB adalah garis singgung dan titik P adalah titik singgung pada lingkaran kecil. Dengan menggunakan kekongruenan segitiga, tunjukkan bahwa titik P adalah titik tengah AB.

Jawaban :

∆AOB adalah segitiga sama kaki dengan OA = OB (jari-jari lingkaran)
sehingga m∠OAB = m∠OBA atau m∠OAP = m∠OBP.
P adalah titik singgung pada lingkaran kecil, maka OP tegak lurus dengan AB
Lihat ∆OAP dan ∆OBP
∆OAP = ∆OBP dan ∆OPA = ∆OPB = 90o
, maka ∆AOP = ∆BOP
Berarti berdasarkan kriteria sisi - sudut - sudut
yaitu: OA = OB, ∆OPA = ∆OPB = 90o
 dan ∆AOP = ∆BOP
maka ∆OAP dan ∆OBP kongruen.
Akibatnya, AP = BP (titik P adalah titik tengah AB)

Sebelum melanjut ke soal berikutnya, bisa kalian tonton terlebih dahulu pembahasan soal hots kesebangunan di bawah ini, jangan lupa juga untuk subscribe, like dan share video ini ya. terima kasih

6. Perhatikan gambar di bawah ini. Pada segitiga ABC, BM tegak lurus dengan AC, CN tegak lurus dengan AB. Panjang BM = CN. Tunjukkan bahwa ∆BCM ≅ ∆CBN

Jawaban :

Gunakan kriteria kekongruenan segitiga siku-siku.
BM = CN (diketahui)
BC = BC (berhimpit)
m∠BMC = m∠CNB = 90o (diketahui)
Jadi, ∆BCM ≅ ∆CBN

7. Perhatikan gambar di bawah ini. Titik M adalah titik tengah QR. Garis XM dan YM masing-masing tegak lurus pada PQ dan PR. Panjang XM = YM. Buktikan bahwa ∆QMX ≅ ∆RMY.

Jawaban :

Buktikan dengan kriteria sisi - sudut - sudut.
Pembuktian Δ QMX kongruen dengan Δ RMY

Sisi yang sama panjang

QM = MR      (diketahui, karena ada tanda)

XQ = YR

MX = MY

Sudut-sudut yang sama besar

∠ MXQ = ∠ MYR        (diketahui, sudut siku-siku)

∠ XMQ = ∠ YMR        (diketahui, sudut berimpit/beradu)

∠ MQX = ∠ MRY

Menentukan kreteria kita lihat yang diketahui pada gambar.

Jadi kreteria : sisi - sudut - sudut

8. Menalar  Diketahui SR//PQ, OP = OQ, OS = OR. Ada berapa pasang segitiga yang kongruen? Sebutkan dan buktikan

Jawaban :

bukti gunakan kriteria kesebangungan segitiga. Ada 3 pasang segitiga kongruen yaitu: ∆POS ≅ ∆QOR, ∆PSR ≅ ∆QRS, dan ∆PSQ ≅ ∆QRP

9. Berpikir Kritis Apakah dua segitiga yang mempunyai tiga pasang sudut-sudut yang bersesuaian sama besar pasti kongruen? Jelaskan dengan alasan yang mendukung jawabanmu.

Jawaban :

Belum tentu, tiga pasang sudut yang bersesuaian sama besar belum menjamin dua segitiga tersebut kongruen.
Contohnya dua segitiga sama sisi
Sudut-sudut yang bersesuaian sama besar, yaitu 60o , tetapi panjang sisi yang bersesuaian tidak selalu sama panjang.

10. Berpikir Kritis Apakah dua segitiga yang mempunyai dua pasang sisi yang bersesuaian sama panjang dan sepasang sudut yang bersesuaian sama besar pasti kongruen? Jelaskan dengan alasan yang mendukung jawabanmu

Jawaban :

Belum tentu, dua segitiga yang mempunyai dua pasang sisi yang bersesuaian sama panjang dan sepasang sudut yang bersesuaian sama besar belum menjamin dua segitiga tersebut kongruen. Kecuali dua sisi yang bersesuaian sama panjang yang mengapit satu sudut yang diketahui sama besar (kriteria sisi – sudut – sisi). Contohnya ∆ABD dan ∆CBD di samping.

(Silakan digambar sendiri) C
AB = CB
BD (pada ∆ABD) = BD (pada ∆CBD)
m∠ADB = m∠CDB (berhimpit)
Tetapi panjang AD ≠ CD.
Dengan kata lain meskipun mempunyai dua pasang sisi yang bersesuaian sama panjang dan sepasang sudut yang bersesuaian sama besar tidak menjamin bahwa ∆ABD tidak sebangun dengan ∆CBD.

11. Membagi Sudut Gambarlah sebuah sudut dan beri nama ∠ABC, kemudian lakukan langkah berikut. a. Dengan menggunakan jangka, bagilah ∠ABC tersebut menjadi dua sama besar.
 (petunjuk: gunakan konsep segitiga kongruen)

Jawaban :

a. Gunakan teknik membagi sudut menjadi dua bagian dengan jangka seperti langkah di bawah ini: (perhatikan gambar)
1. Buat busur lingkaran dengan pusat titik B, sehingga memotong kaki sudut AB di titik D dan memotong kaki sudut BC di titik E.
2. Buat lagi 2 buah busur lingkaran masing-masing dengan pusat di titik D dan E. Perpotongan kedua busur lingkaran tersebut beri nama titik G.
3. Tarik garis dari titik B ke G, sehingga m∠ABG = ∠CBG.

b. 1. Gambarlah garis AD yangsejajar dengan BC.
2. Gambarlah garis CD yang sejajar dengan BA. Sehingga terbentuk bangun jajargenjang ABCD.
3. Tarik garis dari titik B ke D (diagonal jajargenjang ABCD). Jelas bahwa ∆ABD ≅ ∆CBD dengan m∠ABD = ∠CBD.

12. Mengukur Panjang Danau   Chan ingin mengukur panjang sebuah danau tetapi tidak memungkinkan mengukurnya secara langsung. Dia merencanakan suatu cara yaitu ia memilih titik P, Q, R dan mengukur jarak QP dan RP (lihat ilustrasi gambar). Kemudian memperpanjang QP menuju ke Q'dan RP menuju ke R' sehingga panjang QP = PQ' dan RP = PR'. Chan menyimpulkan bahwa dengan mengukur panjang Q'R' dia mendapatkan panjang danau tersebut. Apakah menurutmu strategi Chan benar? Jelaskan.

Jawaban :

Strategi Chan benar. Dia menggunakan konsep dua segitiga kongruen. ∆PQR dijamin sebangun dengan ∆PQ'R' karena memenuhi kriteria kekongruenan dua segitiga sisi – sudut – sisi, yaitu:
PQ = PQ' (diketahui)
m∠QPR = m∠Q'PR’' (bertolak belakang)
PR = PR' (diketahui)
Sehingga, panjang danau QR = Q'R'.

Demikianlah Postingan tentang Soal dan Jawaban Latihan 4.2 Kekongkruenan Dua Segitiga, Matematika Kelas 9, semoga bermanfaat