Soal dan Jawaban Latihan 5.1 Tabung, Matematika Kelas 9
Soal dan Jawaban Latihan 5.1 Tabung, Matematika Kelas 9 ~ m4thguru.info, Selamat berjumpa lagi adik-adik, kali ini kk akan membahasa tentang soal Latihan 5.1 yang berada di halaman 280 hingga 283, soal kk ambil dari buku paket kelas 9 kurikulum 2013 tentang Tabung, Jawaban soal yang ada di blog ini sengaja kk postingkan sebagi bahan referensi untuk adik-adik belajar ya, bukan hanya dijadikan sebagai contekan saja, jadi jawaban soal latihan 5.1 tentang tabung ini adik gunakan sebagai bahan evaluasi setelah adik-adik menjawab soal yang ada di buku paket matematika kelas 9 tentang bangun ruang sisi lengkung, khususnya yaitu tenatang Tabung. semoga postingan kk bermanfaat, jika ada sangahan, kritik dan pesan adik-adik dapat berkomentar di bawah postingan ini, oke cukup sekian pembukaan dari pembahasan soal latihan 5.1 tentang tabung silahkan adik-adik simak atau perhatikan jawaban di bawah ini, dan pelajari dengan cermat, karena pembahasan soal 5.1 Tabung yang ada di blog ini sangat menarik dan dapat dijadikan sebgai referensi buat adik-adik belajar.
Soal dan Jawaban Latihan 5.1 Tabung, Matematika Kelas 9 halaman 280-283
Pembahasan :
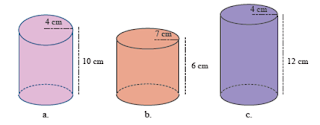
1. a). L = 2πr(r+t)
= 2 . 3,14 . 4 (4 + 10)
= 351,68 cm²
b). L = 2πr(r+t)
= 2 . 3,14 . 7 (7 + 6)
= 571,48 cm²
c). L = 2πr(r+t)
= 2 . 3,14 . 4 (4 + 12)
= 401,92 cm²
d). L = 2πr(r+t)
= 2 . 3,14 . 1 (1 + 8)
= 56,52 cm²
e). L = 2πr(r+t) ⇒ cari r nya dulu
= 2 . 3,14 . 2 (2 + 10)
= 150,72 m²
f). L = 2πr(r+t)
= 2 . 3,14 . 3,5 (3,5 + 20)
= 516,53 cm²
= 2 . 3,14 . 4 (4 + 10)
= 351,68 cm²
b). L = 2πr(r+t)
= 2 . 3,14 . 7 (7 + 6)
= 571,48 cm²
c). L = 2πr(r+t)
= 2 . 3,14 . 4 (4 + 12)
= 401,92 cm²
d). L = 2πr(r+t)
= 2 . 3,14 . 1 (1 + 8)
= 56,52 cm²
e). L = 2πr(r+t) ⇒ cari r nya dulu
= 2 . 3,14 . 2 (2 + 10)
= 150,72 m²
f). L = 2πr(r+t)
= 2 . 3,14 . 3,5 (3,5 + 20)
= 516,53 cm²
.
Ket: V = volume tabung, L = luas permukaan tabung, r = jari-jari tabung,
t = tinggi tabung.
Pembahasan:
2. a). V = 1/4.π.d².t
600π = 1/4 . π . 20² . t
t = 6 cm
b). L = 2πr(r+t)
120π = 2 . π . 5 (5 + t)
12 = 5 + t
t = 7 cm
c). V = 1/4.π.d².t
224π = 1/4 . π . 8² . t
t = 14 cm
d). L = 2πr(r+t)
528π = 2 . π . r (r + 13)
264 = r (r + 13)
r² + 13r - 264 = 0 ⇒ dicari aja r yang memenuhi menggunakan akar-akar persamaan kuadrat.
(r + 24) (r - 11) = 0
r = -24 atau r = 11
600π = 1/4 . π . 20² . t
t = 6 cm
b). L = 2πr(r+t)
120π = 2 . π . 5 (5 + t)
12 = 5 + t
t = 7 cm
c). V = 1/4.π.d².t
224π = 1/4 . π . 8² . t
t = 14 cm
d). L = 2πr(r+t)
528π = 2 . π . r (r + 13)
264 = r (r + 13)
r² + 13r - 264 = 0 ⇒ dicari aja r yang memenuhi menggunakan akar-akar persamaan kuadrat.
(r + 24) (r - 11) = 0
r = -24 atau r = 11
3. Berpikir Kritis. Terdapat suatu tabung dengan jari-jari r cm dan tinggi tabung t cm, dimana r < t. Misalkan tabung tersebut memiliki volume V cm3 dan luas permukaan L cm2 . Apakah mungkin V = L?Jika ya, tentukan nilai 1/r + 1/t
Pembahasan :
Diketahui:
Sebuah tabung berjari-jari r cm dengan tinggi t cm.
r < t
Volume tabung = V cm³
Luas permukaan tabung = L cm²
Ditanyakan:
Apakah mungkin V = L? Jika ya tentukan nilai 1/r + 1/t.
Jawab:
V = π r² t
L = 2 π r (r + t)
Kondisi pada saat volume sama dengan luas permukaan:
V = L
↔ π r² t = 2 π r (r + t)
↔ r t = 2(r + t)
↔ (r + t)/rt = 1/2
↔ r/rt + t/rt = ½
↔ 1/t + 1/r = 1/2
Jadi, mungkin terjadi nilai V = L, yaitu ketika nilai 1/t + 1/r = ½
Sebuah tabung berjari-jari r cm dengan tinggi t cm.
r < t
Volume tabung = V cm³
Luas permukaan tabung = L cm²
Ditanyakan:
Apakah mungkin V = L? Jika ya tentukan nilai 1/r + 1/t.
Jawab:
V = π r² t
L = 2 π r (r + t)
Kondisi pada saat volume sama dengan luas permukaan:
V = L
↔ π r² t = 2 π r (r + t)
↔ r t = 2(r + t)
↔ (r + t)/rt = 1/2
↔ r/rt + t/rt = ½
↔ 1/t + 1/r = 1/2
Jadi, mungkin terjadi nilai V = L, yaitu ketika nilai 1/t + 1/r = ½
4. Tantangan. Gambar di samping
merupakan suatu magnet silinder. Alas dari magnet tersebut dibentuk dari dua lingkaran yang sepusat. Lingkaran yang lebih kecil memiliki jari-jari r1 = 4 cm, sedangkan lingkaran yang lebih besar memiliki jari-jari r2 = 6 cm. Tinggi dari magnet adalah t = 10 cm. Tentukan: a. Luas permukaan magnet. b. Volume magnet.
merupakan suatu magnet silinder. Alas dari magnet tersebut dibentuk dari dua lingkaran yang sepusat. Lingkaran yang lebih kecil memiliki jari-jari r1 = 4 cm, sedangkan lingkaran yang lebih besar memiliki jari-jari r2 = 6 cm. Tinggi dari magnet adalah t = 10 cm. Tentukan: a. Luas permukaan magnet. b. Volume magnet.
Pembahasan :
Diketahui :
jari-jari lingkaran besar= 6 cm
jari-jari lingkaran kecil = 4 cm
tinggi= 10 cm
a. Luas permukaan magnet
= luas penampang luar magnet + luas penampang dalam magnet + 2(luas lingkaran b - lingkaran k)
= 2π r2 . t + 2πr1.t + 2(π r2² - π r1²)
= 2π 6 .10 + 2π 4. 10 + 2(π.6² - π.4²)
= 120π + 80π + 2(36π - 16π)
= 200π + 2(20π)
= 200π + 40π
= 240π
= 240 x 3,14 cm²
= 753,6 cm²
b, Volume magnet
V = Volume tabung besar - volume tabung kecil
= π r² .t - π r1². t
= π.6² . 10 - π 4². 10
= 360π - 160π
= 200π
= 2000 x 3,14
= 6.28 cm³
jari-jari lingkaran besar= 6 cm
jari-jari lingkaran kecil = 4 cm
tinggi= 10 cm
a. Luas permukaan magnet
= luas penampang luar magnet + luas penampang dalam magnet + 2(luas lingkaran b - lingkaran k)
= 2π r2 . t + 2πr1.t + 2(π r2² - π r1²)
= 2π 6 .10 + 2π 4. 10 + 2(π.6² - π.4²)
= 120π + 80π + 2(36π - 16π)
= 200π + 2(20π)
= 200π + 40π
= 240π
= 240 x 3,14 cm²
= 753,6 cm²
b, Volume magnet
V = Volume tabung besar - volume tabung kecil
= π r² .t - π r1². t
= π.6² . 10 - π 4². 10
= 360π - 160π
= 200π
= 2000 x 3,14
= 6.28 cm³
5. Irisan Tabung.
Misalkan terdapat suatu tabung dengan jari-jari r cm dan panjang t cm. Kemudian tabung tersebut dijadikan irisan tabung dengan memotong tabung tersebut menjadi dua bagian yang sama persis dari atas ke bawah. Tentukan rumus untuk menghitung luas irisan tabung tersebut.
Misalkan terdapat suatu tabung dengan jari-jari r cm dan panjang t cm. Kemudian tabung tersebut dijadikan irisan tabung dengan memotong tabung tersebut menjadi dua bagian yang sama persis dari atas ke bawah. Tentukan rumus untuk menghitung luas irisan tabung tersebut.
Pembahasan :
L. permukaan bangun = 1/2 L. permukaan tabung + L. penampang belahan
= 1/2 .2.π.r (r + t) + 2r . t
= π.r (r + t) + 2.r.t
= 1/2 .2.π.r (r + t) + 2r . t
= π.r (r + t) + 2.r.t
6. Tandon Bocor. Terdapat suatu tandon yang berbentuk tabung dengan jari-jari 50 cm tinggi 2 m. Tandon tersebut berisi air sebanyak ¾ dari volume total. Terdapat lubang kecil di dasar tandon tersebut yang menyebabkan air mengalir keluar dengan kecepatan 50 cm3 /detik. Air pada tandon tersebut akan habis setelah ... detik? (anggap π = 3,14).
Pembahasan :
Volume tandon = 3/4 π r² .t
= 3/4 x 3,14 x 50 x 50 x 200
=1.177.500 $cm^3$
waktu air habis di tandon = volume : debit
= 1.177.500 $cm^3$ : 50 $cm^3$/detik
= 23.550 detik
7. Pondasi rumah.
Alas dari pondasi rumah pak Ahmad berbentuk seperti gambar di samping. Jika tinggi pondasi adalah 2 m maka: a. tentukan luas permukaan pondasi, b. tentukan volume pondasi.
Alas dari pondasi rumah pak Ahmad berbentuk seperti gambar di samping. Jika tinggi pondasi adalah 2 m maka: a. tentukan luas permukaan pondasi, b. tentukan volume pondasi.
Pembahasan :
Petunjuk: Hitung terlebih dahulu luas dari alas pondasi. Ubah satuan ke cm.
Luas alas = 30 × 30 – π$(5)^2$ =( 900 – 25π) $cm^2$ = 900 - 78,5 = 821,5 $cm^2$
Luas alas = 30 × 30 – π$(5)^2$ =( 900 – 25π) $cm^2$ = 900 - 78,5 = 821,5 $cm^2$
Keliling Alas = 4 x20 + 2.π.5 = 80 + 10π = 80 + 31,4 = 111,4 cm
Luas permukaan pondasi = 2 Luas alas + keliling alas x t = 2 x 821,5 + 111,4 x 200 = 1643 + 22.280 = 23.823 $cm^2$
Volume = Luas alas × tinggi
= 821,5× 200 = 164.300 $cm^3$
Volume = Luas alas × tinggi
= 821,5× 200 = 164.300 $cm^3$
8. Analisis Kesalahan. Rudi menghitung volume tabung dengan diameter 5 cm dan tinggi 12 cm. Rudi menghitung V = (12)2 (5) = 720 Sehingga diperoleh volume tabung adalah 720 cm3 . Tentukan kesalahan yang dilakukan Budi
Pembahasan :
Diketahui :
diameter(d) = 5 cm
r= 1/2 x 5 cm
r = 2,5 cm
tinggi (t) = 12 cm
Ditanya :
tentukan kesalahan yang dilakukan Budi ?
Jawab :
rumus volume tabung = π x r² x t
V = 3,14 x 2,5 x 2,5 x 12
V =235,5 cm ³
jadi volume tabung sebenarnya 235,5 cm³
maka kesalahan yang dilakukan budi yaitu salah menggunakan rumus , rumus budi adalah V = t² x d seharusnya rumus yg digunakan adalah V = π x r² x t
diameter(d) = 5 cm
r= 1/2 x 5 cm
r = 2,5 cm
tinggi (t) = 12 cm
Ditanya :
tentukan kesalahan yang dilakukan Budi ?
Jawab :
rumus volume tabung = π x r² x t
V = 3,14 x 2,5 x 2,5 x 12
V =235,5 cm ³
jadi volume tabung sebenarnya 235,5 cm³
maka kesalahan yang dilakukan budi yaitu salah menggunakan rumus , rumus budi adalah V = t² x d seharusnya rumus yg digunakan adalah V = π x r² x t
9. Tabung miring. Pada gambar di bawah terdapat dua buah bangun sisi lengkung.
Sebelah kiri merupakan tabung dengan jari-jari r dan tinggi t. Sebelah kanan merupakan bangun ruang sisi lengkung yang diperoleh dari tabung sebelah kiri dengan menggeser tutup ke sebelah kanan, selanjutnya disebut dengan tabung miring. Tabung miring tersebut memiliki jari-jari r dan tinggi t.
Sebelah kiri merupakan tabung dengan jari-jari r dan tinggi t. Sebelah kanan merupakan bangun ruang sisi lengkung yang diperoleh dari tabung sebelah kiri dengan menggeser tutup ke sebelah kanan, selanjutnya disebut dengan tabung miring. Tabung miring tersebut memiliki jari-jari r dan tinggi t.
a. Tentukan suatu metode untuk mendapatkan rumus dari volume tabung miring tersebut.
b. Apakah volume rumus tabung miring sama dengan volume tabung? Jelaskan analisismu.
Pembahasan :
a. Salah satu metode adalah dengan membuat tumpukan koin yang membentuk tabung miring.
b. Sama, karena kaidah volume adalah luas alas dikalikan dengan tinggi. Dengan merubah tabung menjadi tabung miring tidak merubah alas dan tingginya, sehingga tidak terjadi perubahan volume.
b. Sama, karena kaidah volume adalah luas alas dikalikan dengan tinggi. Dengan merubah tabung menjadi tabung miring tidak merubah alas dan tingginya, sehingga tidak terjadi perubahan volume.
10. Kaleng susu. Suatu perusahaan susu memiliki kotak susu ukuran 40 cm × 60 cm × 20 cm. Kapasitas maksimal kotak tersebut adalah 48 kaleng susu. Jarijari kaleng susu adalah r cm dan tingginya t cm. Perusahaan tersebut membuat peraturan:
i. Nilai r dan t harus bilangan bulat.
ii. Luas permukaan kaleng tersebut harus seminimal mungkin. Tentukan nilai r dan t.
Pembahasan :
Perhatikan gambar berikut ini
Gambar di atas merupakan alas kotak susu dengan ukuran 40 cm × 60 cm, tiaptiap persegi kecil berukuran 10 cm × 10 cm. Siswa dapat membuat lingkaran dengan jari-jari 5 cm (warna biru) atau dengan jari-jari 10 cm (warna merah).
i. Ketika r = 5 cm, diperoleh 24 lingkaran. Karena kapasitas kotak tersebut adalah 48 kaleng susu, maka tinggi kaleng susu adalah t = 20 × ( 24/48 ) = 10. Diperoleh luas permukaan kaleng = 2πr(r + t) = 2π(5)(5 + 10) = 150π
ii. Ketika r =10 cm, diperoleh 12 lingkaran. Karena kapasitas kotak tersebut adalah 48 kaleng susu, maka tinggi kaleng susu adalah t = 20 × ( 12/48 ) = 5. Diperoleh luas permukaan kaleng = 2πr(r + t) = 2π(10)(10 + 5) = 300π Luas permukaannya minimal saat r = 5 cm, t = 10 cm.
i. Ketika r = 5 cm, diperoleh 24 lingkaran. Karena kapasitas kotak tersebut adalah 48 kaleng susu, maka tinggi kaleng susu adalah t = 20 × ( 24/48 ) = 10. Diperoleh luas permukaan kaleng = 2πr(r + t) = 2π(5)(5 + 10) = 150π
ii. Ketika r =10 cm, diperoleh 12 lingkaran. Karena kapasitas kotak tersebut adalah 48 kaleng susu, maka tinggi kaleng susu adalah t = 20 × ( 12/48 ) = 5. Diperoleh luas permukaan kaleng = 2πr(r + t) = 2π(10)(10 + 5) = 300π Luas permukaannya minimal saat r = 5 cm, t = 10 cm.
Video Pembahasan Latihan 5.1 Tabung, matematika Kelas 9
Demikianlah pembahasan soal dan Jawaban Latihan 5.1 Tabung, Matematika Kelas 9, semoga bermanfaat