Soal dan Jawaban Latihan 3.3 Perputaran (Rotasi) , Matematika Kelas 9
Soal dan Jawaban Latihan 3.3 Perputaran (Rotasi) , Matematika Kelas 9.~ m4thguru.info, assalamualaikum Wr Wb, Salam Sejahtera untuk kita semua, kali ini kkaktri akan postingan lagi tentang soal dan kunci Jawaban Soal Ayo kita Berlatih Matematika kelas 9 yang diambil dari buku paket matematika kurikulum 2013 revisi 2018. untuk soal kali ini tentang memahami posisi garis terhadap sumbu x dan sumbu y, soal ada di halaman 169-171 buku matematika kelas 9 Bab 3 tentang Transformasi. untuk jawaban kkaktri sendiri yang menjawab dan sengaja di share sebagai bahan evaluasi adikadik setelah mengerjakan soal tersebut.
Soal dan Jawaban Latihan 3.3 Perputaran (Rotasi) , Matematika Kelas 9.
Soal
1. Jelaskan apakah gambar yang berwarna biru merupakan hasil rotasi dari gambar yang berwarna merah. Jika ya, berapa besar sudut rotasi dan bagaimana arah dari rotasi tersebut?
Pembahasan:
a. Tidak
b. Ya. $90^o$ berlawanan arah jarum jam
c. Ya. $180^o$
2. Segi empat PQRS berkoordinat di P (2, –2), Q (4, –1), R (4, –3) dan S (2, –4). Gambarlah bayangan PQRS pada rotasi $90^o$ berlawanan arah jarum jam yang berpusat di titik asal.
Pembahasan:
Koordinat bayangan hasil rotasinya adalah P'(2, 2), Q'(1, 4), R'(3, 4) dan S'(4, 2)
3. Salinlah ∆WAN berikut. Kemudian rotasikan segitiga tersebut sebesar 90o searah jarum jam yang berpusat di titik H.
Pembahasan
4. Gambar bayangan rotasi bangun berikut dengan sudut 90o jika diketahui arah dan pusat rotasi. Tentukan koordinat titik-titik bayangannya. ∆WAN dengan W (–4, 1), A (–2, 1), dan N (–4, –3) berlawanan arah jarum jam dengan pusat rotasi di titik N
Pembahasan:
Koordinat bayangan hasil rotasinya adalah W' (–8, –3), A' (–8, –1) dan N' (–4, –3)
5. Gambar bayangan tranformasi untuk setiap segitiga berikut dengan mencerminkan segitiga pada garis yang diketahui. Bayangan akhir dari setiap bangun juga merupakan hasil rotasi. Tentukan koordinat bayangan dan sudut rotasi.
a. ∆TUV dengan T (4, 0), U (2, 3), dan V (1, 2) direfleksikan pada sumbu-y dilanjutkan sumbu-x.
b. ∆KLM dengan K (5, 0), L (2, 4), dan M (–2, 4) direfleksikan pada garis y = x dilanjutkan sumbu-x.
c. ∆XYZ dengan X (5, 0), Y (3, 4), dan Z (–3, 4) direfleksikan pada garis y = -x dilanjutkan garis y = x.
Pembahasan:
a. Koordinat bayangannya adalah T' (–4, 0), U' (–2, –3) dan V' (–1, –2). Sudut rotasi $180^o$
b. Koordinat bayangannya adalah K' (0, –5), L' (4, –2) dan M' (4, 2). Sudut rotasi $90^o$ searah jarum jam
c. Koordinat bayangannya adalah X' (–5, 0), Y' (–3, –4) dan Z' (3, –4). Sudut rotasi 180
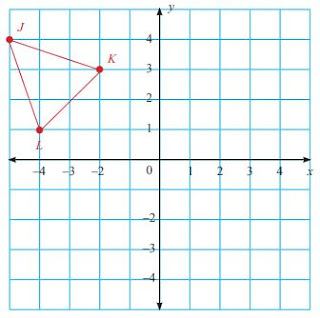
6. Diketahui segitiga JKL seperti pada gambar di bawah ini.
a. Rotasikan segitiga JKL dengan sudut rotasi $90^o$ searah jarum jam dengan pusat rotasi titik asal (0, 0). Berapakah koordinat titik sudut dari segitiga J’K’L’ yang merupakan bayangan dari segitiga JKL?
b. Rotasikan segitiga JKL dengan sudut rotasi180o searah jarum jam dengan pusat rotasi titik asal (0, 0). Berapakah koordinat titik sudut dari segitiga J’K’L’ yang merupakan bayangan dari segitiga JKL?
Pembahasan:
a. Koordinat bayangannya adalah J' (4, 5), K' (3, 2) dan L' (1, 4)
b. Koordinat bayangannya adalah J' (5, –4), K' (2, –3) dan L' (4, –1)
7. Diketahui segitiga RST dengan koordinat titik sudut di R (3 ,6), S (–5, 2) dan T (3, –3). Gambar bayangan hasil transformasinya jika diketahui segitiga tersebut:
a. Dirotasi $90^o$searah jarum jam yang berpusat di titik asal kemudian dicerminkan terhadap sumbu-y.
b. Dirotasi $90^o$ berlawanan arah jarum jam yang berpusat di titik asal kemudian didilatasi dengan faktor skala 2 berpusat di titik asal.
c. Dirotasi $180^o$ berlawanan arah jarum jam yang berpusat di titik asal kemudian ditranslasi (4 5) setelah itu dicerminkan terhadap sumbu-x
Pembahasan:
a. Bayangan segitiga RST hasil rotasi adalah R' (6, –3), S' (2, 5) dan T' (–3, –3). Setelah dicerminkan terhadap sumbu-y, maka koordinat bayangannya adalah R'' (–6, –3), S'' (–2, 5) dan T'' (3, –3)
b. Bayangan segitiga RST hasil rotasi adalah R' (–6, 3), S' (–2, –5) dan T' (3, 3). Setelah didilatasi maka koordinat bayangannya adalah R'' (-12, 6), S'' (–4, –10) dan T'' (6, –6)
c. Bayangan segitiga RST hasil rotasi adalah R' (–3, –6), S' (5, –2) dan T' (–3, 3). Setelah ditranslasi maka koordinat bayangannya adalah R'' (1, –1), S'' (9, 3) dan T'' (1, 8), kemudian setelah dicerminkan terhadap sumbu-x koordinat akhir bayangannya adalah R''' (1, 1), S''' (9, –3) dan T''' (1, –8)
Demikianlah Soal dan Jawaban Latihan 3.3 Perputaran (Rotasi) , Matematika Kelas 9. semoga bermanfaat